腎臓③:計算に必要な基礎知識、濃縮率の求め方
『この記事について』
腎臓の計算問題は、
以下の4つに大別できます。
・濃縮率の計算
・原尿量の計算
・再吸収量の計算
・再吸収率の計算
この記事の前半では、
上記4つの、全ての計算問題を
攻略するのに必要な
・腎臓の基礎知識
・濃度と密度
について解説します。
記事の後半では、
原尿量の計算にもつながる、
濃縮率の計算
について解説します。
その他の計算については、
以下の記事で扱っています。
→ 原尿量の計算
→ 再吸収量、再吸収率の計算
→ グルコース排出量のグラフ
目次
1:計算に必要な、腎臓の基礎知識
腎臓の計算問題を解くには、
腎臓の働きである
・ろ過
・再吸収
の仕組みの理解が必須です。
詳しくは、
記事「腎臓②:腎臓の働き」で
扱っていますが、
この記事では、
計算に必要な最低限の知識だけを
さらっと確認していきましょう。
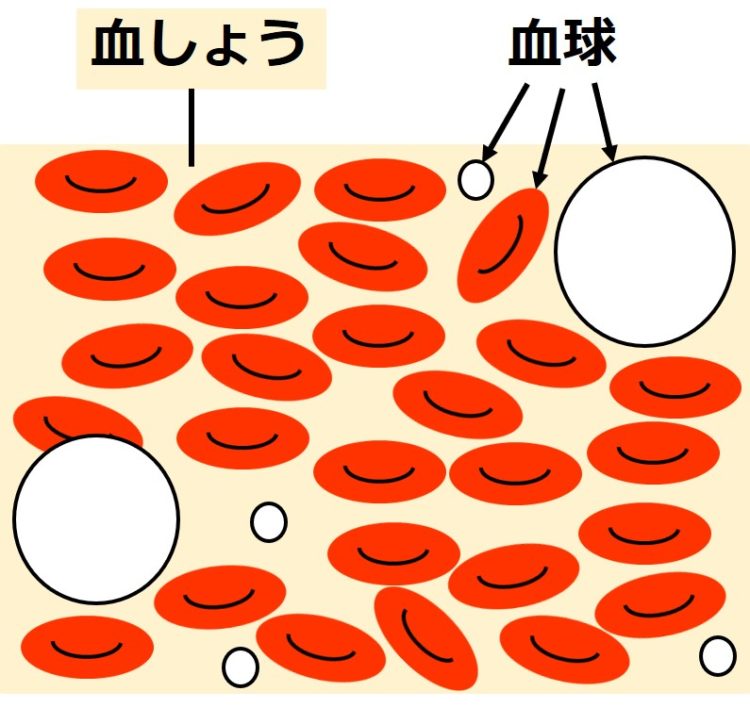
血液の成分は、
・赤血球、白血球などの細胞(血球と総称される)
・血しょう(水を中心とした液体の成分)
に分けられます(下図)。
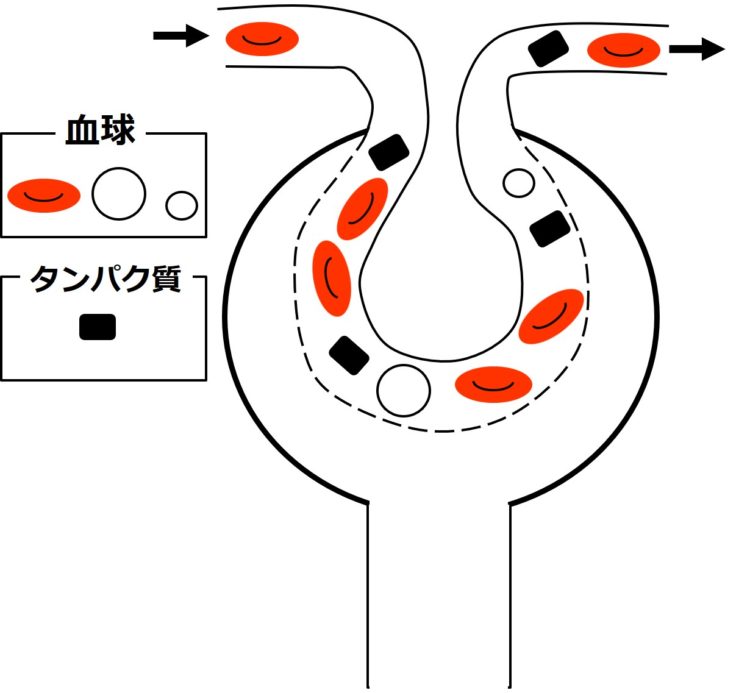
腎臓内の糸球体(しきゅうたい)と
呼ばれる部位の血管は、
壁に小さな孔(あな)が空いています。
そして、血液がこの血管を流れる時に、
血しょうの一部が孔を通って
血管の外へ出るのです。
赤血球などの血球は、大きいため
外へ出られません。
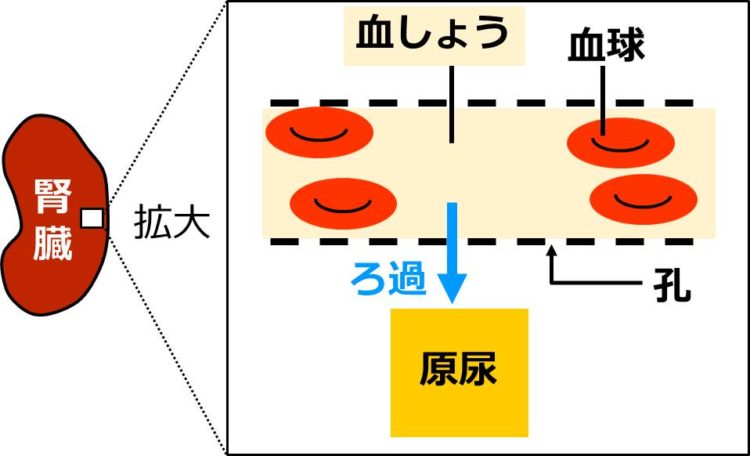
このように、腎臓内で
血しょうの一部が
血管外へ出る仕組みのことを
ろ過
と言います。
ろ過の結果、
血管外へ出た液体のことを
原尿(げんにょう)と呼びます。
(下図:孔の開いた血管で行われる ろ過)
原尿の成分には、
体にとって必要な成分と
不要な成分の両方が含まれています。
原尿の成分のうち、一部の成分
(主に体にとって必要な成分)は、
再び血管内へと戻されます。
この仕組みのことを
再吸収
と言います。
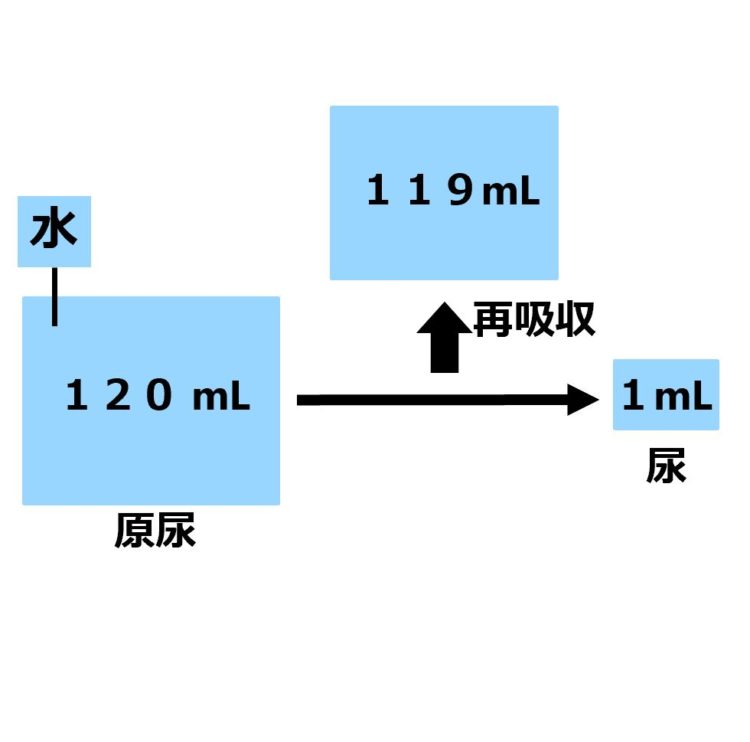
再吸収は、原尿が
細尿管(さいにょうかん)という管などを
通るときに行われます。
再吸収の後に残った液体を
尿と呼び、
腎臓を出たのち、
ぼうこう などを経て体外へと
排出されます(下図)。
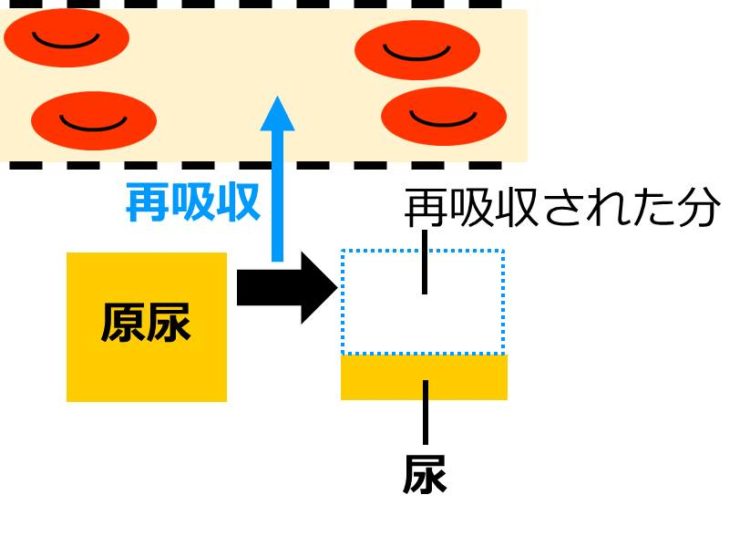
つまり、腎臓では、
まず、大まかに血しょうの一部を血管外へと
取り出し、後から、体に必要な物質を回収して、
不要な物質を尿として捨て去っているのです。
ちょうど、机の引き出し中を大掃除する際に、
一度全部モノを取り出して、後から、必要なものを
引き出しの中に戻すことと似ています。
では次に、
濃度と密度の解説に
入りましょう。
2:濃度と密度
2-1. 体積濃度と質量パーセント濃度
濃度というのは、
溶液に含まれる溶質の割合
のことです。
血しょう、原尿、尿などが
溶液にあたります。
腎臓の計算問題では、
・体積濃度:単位(mg/mLなど)
・質量パーセント濃度:単位(%)
の2つが頻出します。
まずは、
これらの濃度の扱い方を
マスターしましょう。
2-2. 体積濃度
体積濃度というのは、
溶質の質量を、溶液の”体積”で割って
求められる濃度のことです(下図)。

例えば、
1mLの尿(溶液)に、
尿素という溶質が20 mg
含まれるとき、
この尿における
尿素の体積濃度は、
20 mg ÷ 1 mL = 20 mg/mL
となります。
逆に言えば、
〇〇 mg/mL
という濃度表記は、
1 mLの溶液に
〇〇 mgの溶質が含まれますよ
という情報を、
簡単に書き表した
ものなのです。
例えば、
『尿中の尿素濃度が
20 mg/mL のとき、
2 mL の尿に含まれる
尿素の質量は何 mgか?』
という問題に対しては、
20 mg/mL × 2 mL = 40 mg
と計算することが
出来ます。
他にも、
〇〇 mg/100mL
などの表記が見られることも
ありますが、
これは、
100 mLの溶液に
〇〇 mgの溶質が含まれますよ
という意味なのです。
例題
①尿中のナトリウムイオン濃度が
3.1 mg/mLのとき、
この尿10 mLに含まれる
ナトリウムイオンは何 mgか?
②血しょう中の尿素濃度が
1800 mg/100mLのとき、
血しょう30 mLに含まれる
尿素は何 mgか?
解答
①3.1 mg/mL × 10 mL = 31 mg
②1800 mg/100mL
= 18 mg/mL なので、
18 mg/mL × 30 mL
= 540 mg
2-3. 質量パーセント濃度
質量パーセント濃度というのは、
溶質の質量を溶液の”質量”で割り、
100をかけることで
求められる濃度のことです。
単位は、%(パーセント)です(下図)。

この公式は、
溶質の質量
= 溶液の質量 × 質量パーセント濃度 / 100
と変形でき、
腎臓の計算では
この形でよく使います。
例題
尿中の尿素濃度が2 %のとき、
この尿70 gに含まれる尿素は何 gか?
解答
尿素の質量(g)
= 尿の質量(g) × 尿の質量パーセント濃度 / 100
= 70 g × 2 / 100
= 1.4 g
2-4. 密度
質量パーセント濃度は、
しばしば、密度(みつど)と共に
問題文に登場します。
密度は、以下の式で
表されます。
密度 = 質量 ÷ 体積
この式は、
質量 = 体積 × 密度
と書き換える
ことができ、
腎臓の計算問題では、
体積を質量に変換する
ために、よく利用します。
例題
尿中の尿素濃度が2 %のとき、
この尿80 mLに含まれる尿素は何 gか?
ただし、尿の密度は1 g/mL とする。
解答
2-3. 質量パーセント濃度で
解説したように、
尿素の質量(g)
= 尿の”質量(g)” × 尿の質量パーセント濃度 / 100
である。
尿の密度を用いると、
尿の質量(g)
= 尿の体積 × 尿の密度
= 80 mL × 1 g/mL
= 80 g
となる。
よって、
尿素の質量(g)
= 尿の質量(g) × 尿の質量パーセント濃度 / 100
= 80 g × 2 / 100
= 1.6 g
と求まる。
・・・・・・・・・・・・
では、次の項目から
濃縮率の計算に入りましょう。
3:濃縮率
3-1. この問題を解けるようになろう!
この項目を読み終えた時に、
次のような問題を自力で解ける
レベルを目指して行きましょう。
・・・・・・・・・・・・・・
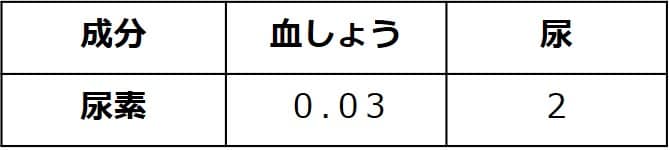
サンプル問題1
ある人の、血しょう中と尿中の
尿素濃度(単位:%)が下表のようで
あるとする。
尿素の濃縮率を求めなさい。
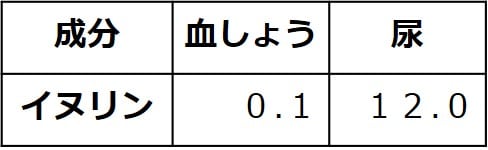
サンプル問題2
ある人のイヌリン濃度(単位:mg/mL)が
下表のようであったとする。
イヌリンの濃縮率を求めなさい。
・・・・・・・・・・・・・・・
3-2. 濃縮率の求め方
ある物質の尿中の濃度を
その物質の血しょう中の
濃度で割った値を、
その物質の
濃縮率(のうしゅくりつ)
と言います(下図)。

濃縮率は、
ある物質が、
血しょうから尿が作られる過程で
何倍に濃縮されたか
を表します。
このため濃縮率は、
〇〇倍
と表記される
ことがあります(※)。
※:倍をつけずに、
単に数値だけで表記して
問題ありません。
例として、尿素という
物質を取り上げて、
濃縮率の計算方法を、
解説しましょう。
ある人の
血しょう中の尿素濃度と
尿中の尿素濃度が、
・血しょう中:0.03%
・尿中:2.0%
だったとします。
この場合の
尿素の濃縮率は、
尿中の尿素濃度 ÷ 血しょう中の尿素濃度
= 2.0 % ÷ 0.03 %
≒ 67 (倍)
となり、
血しょうから尿が作られる過程で、
尿素は、約67倍に濃縮された
ことがわかります。
3-3. 体に必要な物質の濃縮率と老廃物の濃縮率
血しょう中に含まれる物質は、
・体に必要な物質
⇒ 水、ナトリウムイオンなど
・老廃物(ろうはいぶつ:体に不要な物質)
⇒ 尿素など
に分けられます(下図)。
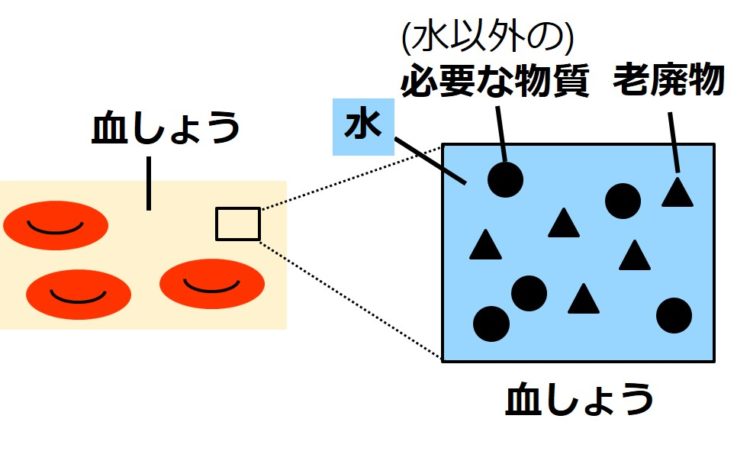
そして、腎臓は、
尿中に老廃物を高濃度につめ込んで
効率よく排出しているのです。
このことは、濃縮率の計算結果にも
表れています。
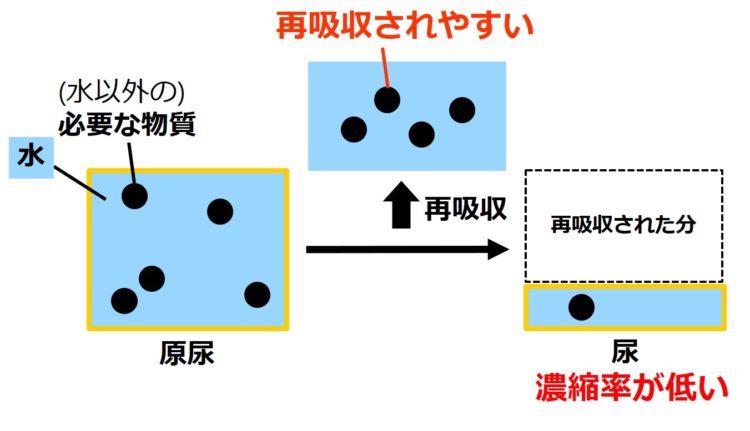
血しょうがろ過されて生じた
原尿の成分のうち、
体に必要な物質は
再吸収されやすく、
老廃物は
再吸収されにくい
という傾向があります。
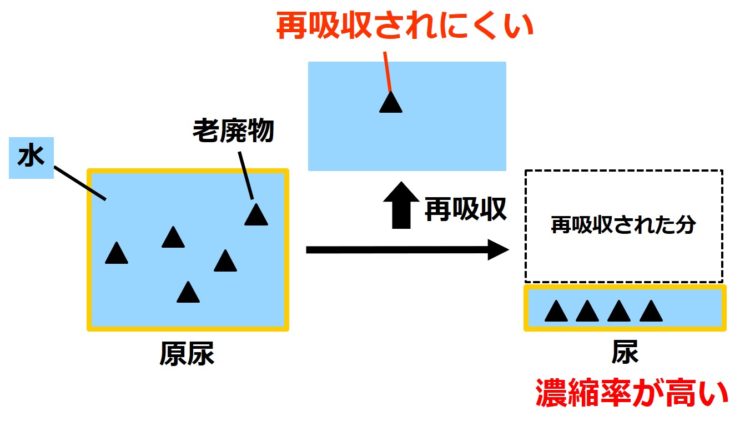
このため、
濃縮率を比べてみると、
老廃物の濃縮率は、
体に必要な物質の濃縮率よりも
高くなる傾向がある
のです(下図)。
例えば、
細胞の働きに欠かせない
ナトリウムイオンの濃縮率は、
1.2(倍※)くらいです。
※:体の状態で多少変動する
一方で、老廃物である
尿素の濃縮率は、
先ほど計算したように
67(倍)にもなるのです。
腎臓が、いかに効率よく
老廃物を排出しているかが
分かりますね。
・・・・・・・・・・・
さて、これで
濃縮率の解説は以上ですが、
自分の力で計算問題に
取り組んでみることで、解く力が
より一層、身についていきます。
次の項目の確認問題に
挑戦してみましょう。
※:スマホ、タブレット端末でのご利用の方へ
記事の最下部には、
「おすすめの人気記事ベスト5」
(【最重要】2021共通テスト『生物基礎』攻略法など)
の一覧も記載してあります。
4:確認問題
確認問題1
ある人の、
・カリウムイオン(細胞の働きに必要な物質)
・クレアチニン
・尿素
の濃度(単位:%)が、
下表のようであるとする。
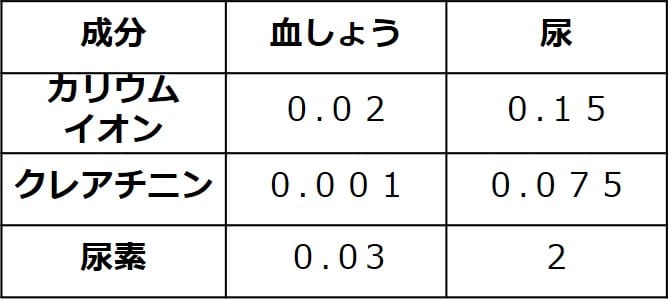
①それぞれの物質の濃縮率を求めなさい。
(尿素は小数点以下を四捨五入)
②濃縮率で判断すると、クレアチニンは、
体に必要な物質と老廃物のどちらで
あると思われるか答えなさい。
解答

(単位:%)
①それぞれの物質の濃縮率を求めなさい。
(尿素は小数点以下を四捨五入)
カリウムイオンの濃縮率
= 0.15 / 0.02 = 7.5(倍)
クレアチニンの濃縮率
= 0.075 / 0.001 = 75(倍)
尿素の濃縮率
= 2 / 0.03 ≒ 67(倍)
②濃縮率で判断すると、クレアチニンは、
体に必要な物質と老廃物のどちらで
あると思われるか答えなさい。
老廃物
・・・・・・・・・・・・・・・・・・・
確認問題2
ある人のイヌリン濃度(単位:mg/mL)が
下表のようであったとする。

イヌリンの濃縮率を求めなさい。
解答

(単位:mg/mL)
イヌリンの濃縮率を求めなさい。
12.0 / 0.1 = 120(倍)
※イヌリンは、
次の記事のテーマである
原尿量の計算で用いられる物質。
・・・・・・・・・・・・・・・・・・・
⇒ つづく記事
「腎臓④:イヌリンを用いた原尿量の求め方」
「腎臓⑤:再吸収量の計算、再吸収率の計算」
「腎臓⑥:グルコース排出量のグラフ」