腎臓④：イヌリンを用いた原尿量の求め方

この記事は、

・典型的な原尿量の計算問題を１分で解く方法
・その方法の理解を促すための解説

からなっています。

１分で解く方法の解説自体は
すぐに終わり、典型的な問題なら
それで解けるようになるでしょう。

ただ、入試ではふつう、
ひとひねりある問題が出題されます。

そうした問題にも対応できるよう、
なぜ、そうした方法で解けるのか、
その理解を促す解説が記事の大半を占めています。

目次

１：この記事で目指すレベル

この記事では、
腎臓分野で頻出する、
以下のような原尿量の計算問題を
スラスラ解けるレベルを目指します。

・・・・・・・・・
サンプル問題
ある人の、血しょう、原尿、尿の
イヌリン濃度が下表のようであるとする。

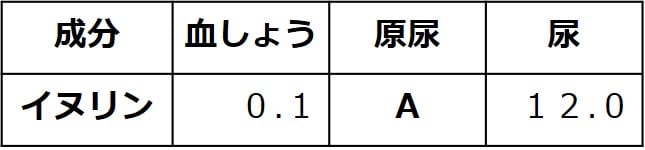
(単位：％)
また、腎臓で１分間に
作られる尿量が１ mLであるとする。

①表の空欄Ａに入る濃度を答えなさい。

②１分間に作られる原尿量は
何 mL であるか求めなさい。

③１日に作られる原尿量は
何 L であるか求めなさい。

・・・・・・・・・

では、さっそく
解説に入りましょう。

目次へ戻れるボタン

２：原尿量は１分で求まる。

先ほど、サンプルで見たような
典型問題であれば、

３つのことを押さえておくだけで、
原尿量は１分で求まります。

その、３つの事というのは、、、

①：
血しょう中のイヌリン濃度　
＝　原尿中のイヌリン濃度　

②：
原尿量　＝　尿量　×　イヌリンの濃縮率(※)

※：濃縮率ってなに？？

③：
②の式では、時間をそろえる。

です。

実際に求めてみましょう。

以下、サンプル問題。

ある人の、血しょう、原尿、尿の
イヌリン濃度が下表のようであるとする。

(単位：％)
また、腎臓で１分間に
作られる尿量が１ mLであるとする。

１：表の空欄Ａに入る濃度を答えなさい。

先ほどの①から、A＝０.１です。

２：１分間あたりの原尿量を求めなさい。

先ほどの②の公式
原尿量　＝　尿量　×　イヌリンの濃縮率

に当てはめます。

ただし、時間をそろえます。
求めたいのは、”１分間あたりの”原尿量なので、
尿量も”１分間あたりの”尿量を代入します。

１分間の尿量は１ｍLであると書いてあります。
また、
イヌリンの濃縮率
＝　尿中のイヌリン濃度÷血しょう中のイヌリン濃度
＝　１２.０÷０.１
＝　１２０　です。

よって、
１分間あたりの原尿量
＝　１ｍL　×　１２０　＝　１２０ｍL

となります。

このように、
典型的な問題ならば、
原尿量はすぐに求まります。

ボンボ

うぁ、公式を使えば簡単なんだなぁ。
でも、どうして原尿量なんて計算するの？
それに、イヌリンって、、、何？

それは少し長い話になります。

でも、そういったことをしっかり理解していると、
入試などで、ひとひねりされた問題が出ても、
対応できますよ！

次から、それらの解説に入りましょう。

目次へ戻れるボタン

３：原尿量を知ると、腎臓の働き具合がわかる

一定の時間内に
腎臓全体で作られる
原尿の量は、

腎臓がしっかり
働いているかどうかを示す
重要なデータです。

腎臓がしっかり働いていると、
血液中の老廃物が、腎臓を通して
体外へ多く排出されます(下図)。

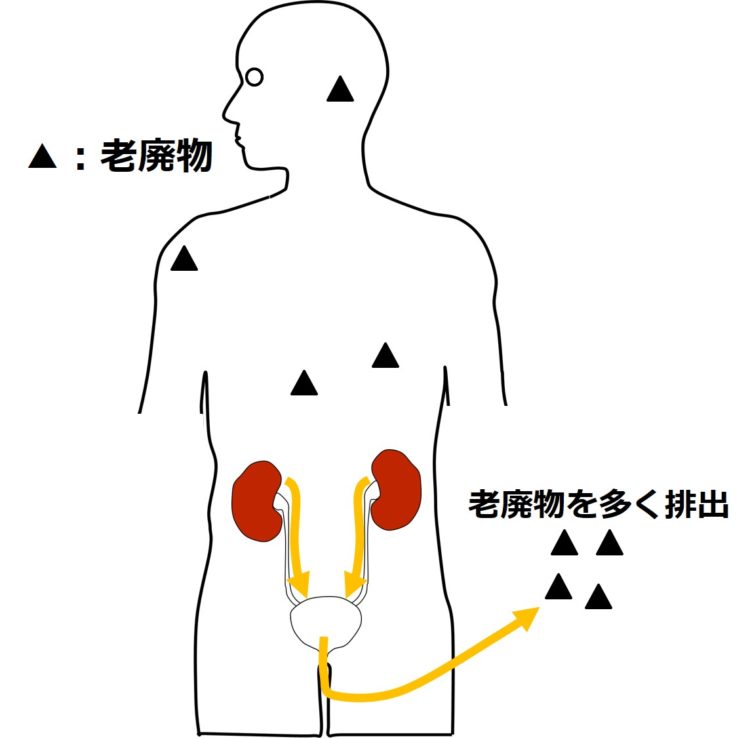
しかし、腎臓の機能が低下して、
作られる原尿量が減ると
体外へ排出できる老廃物の量も減ります。

その結果、体液中に老廃物がたまり
適切な体内環境を保つことが
出来なくなってしまうのです(下図)。

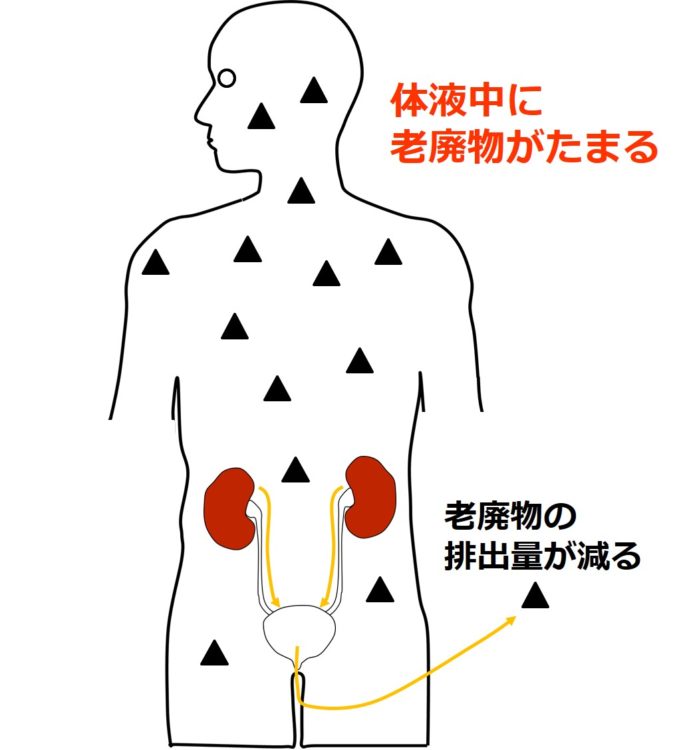
そうなると、体がだるくなったり
最悪、心臓が止まってしまったりと
様々な悪影響が出ます。

このため、特に
腎臓の機能が低下している
可能性がある人の体調管理にとって、

原尿量を調べることは
とても重要なのです。

目次へ戻れるボタン

４：原尿量の計算に利用されるイヌリン

原尿は、腎臓にある
とても小さな構造内で
作られるため、

原尿量を直接測定する
ことは困難です。

では、

どのようにして
原尿量を調べるのでしょうか？

現在、多く用いられているのは
原尿量を計算で求める方法です。

”ある特徴”を持った物質を
利用することで、

原尿量を簡単に
計算することが出来ます。

その特徴というのは、

腎臓において

・ろ過される
・全く再吸収されない

ということです。

そして、このような
特徴を持つ物質として
主に利用されているのが、

植物に由来する

イヌリン

という物質なのです。

目次へ戻れるボタン

５：イヌリンを用いた原尿量の求め方

ある人の腎臓で、

１分間に作られる原尿量(mL)

を知りたいとしましょう。

まずは、
イヌリンを血液中に
注射します(下図)。

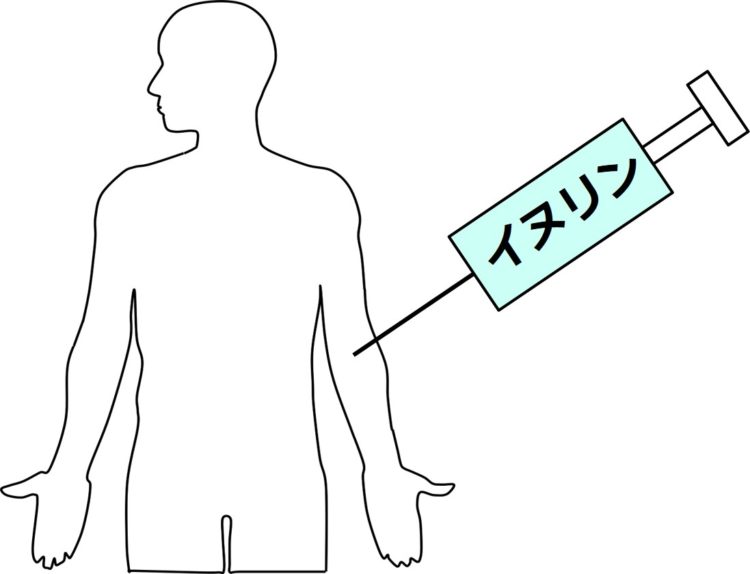
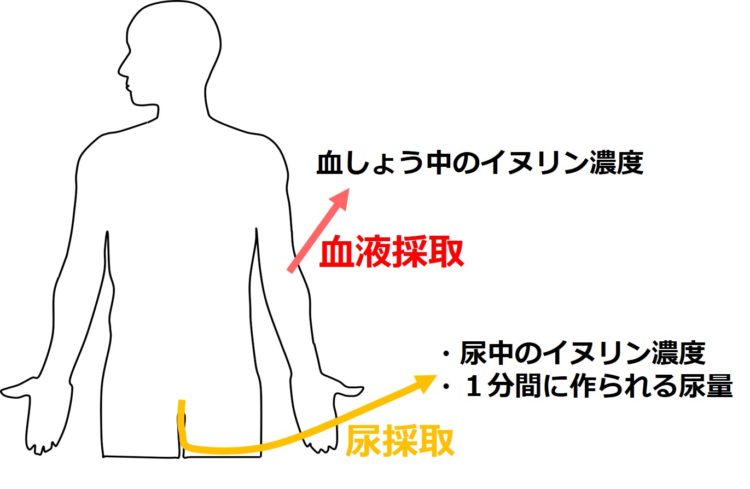
その後、
血液と尿を採取して、

・血しょう中のイヌリン濃度
・尿中のイヌリン濃度
・腎臓で１分間につくられる尿量(mL)※

を調べます(下図)。

※：例えば、３０分毎に尿をとって、
尿量を３０で割って計算します。

その結果、
次のような数値が
得られたとしましょう。

〇イヌリン濃度

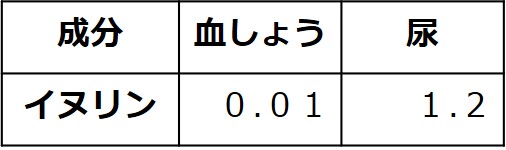
※単位：％

〇１分間に作られる尿量：１ ｍＬ

これらの数値から、
１分間に作られる原尿量(mL)を
計算することが出来ます。

5-1.公式を用いた原尿量の求め方

まずは、以前にも解説した、
原尿量をラクに計算する方法を
もう一度簡単にまとめておきましょう。

それは、

原尿量　＝　尿量　×　イヌリンの濃縮率

です。

原尿量と尿量の時間(何分あたりか)を
そろえることに注意しましょう。

※：濃縮率について　→　「濃縮率」

この公式を用いると、

１分間に作られる原尿量(mL)
＝　１分間に作られる尿量　×　イヌリンの濃縮率
＝　１ mL　×　１２.０ / ０.０１
＝　１２０ mL

と、楽に計算が出来ます。

でも、
数学などと同様に、

便利な公式  “だけ” で
勝負していると、

公式を用いることが出来ない
問題に出会った時に、

お手上げ状態に
なってしまいます。

そうならない様に、
公式を使わずに原尿量を求める
方法を解説しましょう。

その解説の中で、
先ほどの公式も必然的に
導かれてきます。

目次へ戻れるボタン

5-2. 公式を用いずに原尿量を計算する方法

イヌリンに限らず、

腎臓でろ過される
物質の濃度は、

ろ過の前後で
ほぼ変わらず、

血しょう中の濃度 ＝ 原尿中の濃度

と見なすことが出来ます。

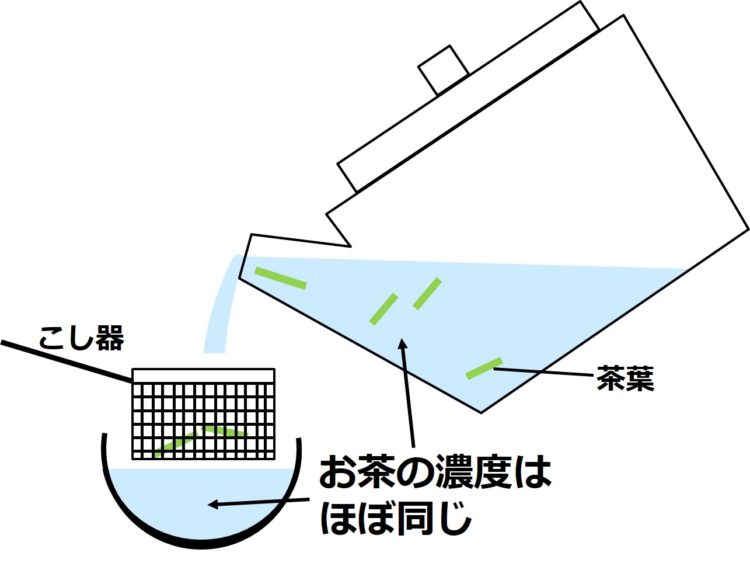
これは、
茶葉が混ざったお茶を、

茶葉を取り除く こし器(ろ過器)を
通して茶碗に注いでも、

お茶の濃さは変わらない
ことと似ています(下図)。

従って
イヌリン濃度は、

血しょう中のイヌリン濃度
＝ 原尿中のイヌリン濃度

とみなすことが
出来るのです(下表)。

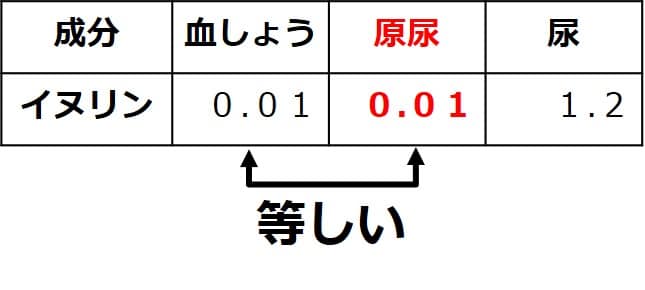
※単位：％

上表から、
尿中のイヌリン濃度は
原尿中のイヌリン濃度に比べて

１.２ ％　÷　０.０１ ％

＝ １２０ 倍　濃いとわかります。

また、
イヌリンのように、

全く再吸収されない
物質では、

原尿中に含まれる物質の
全てが尿中に残るため、

原尿中の質量 ＝ 尿中の質量

となります(下図)。

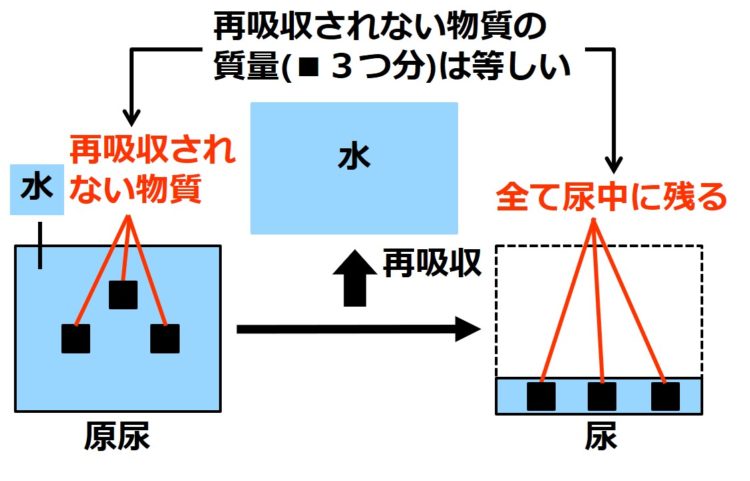
そのため、

全く再吸収されない物質の
尿中の濃度が、
原尿中の濃度に比べて濃くなるのは、

水が再吸収されたことによる

と考えることが出来ます。

つまり、

尿中のイヌリン濃度が
原尿中のイヌリン濃度に比べて
１２０倍濃くなったのは、

原尿中の水が再吸収されて、
尿の体積(尿量)が、原尿の体積(原尿量)の
１２０分の１になったため

と考えることが出来るのです(下図)。

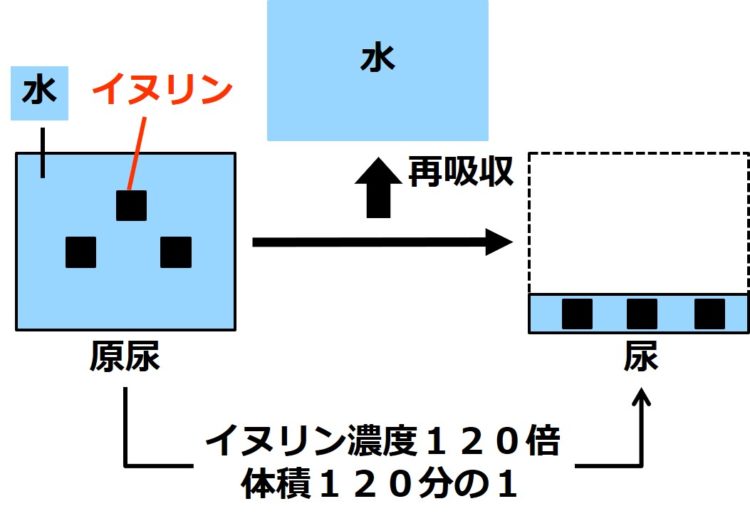
これは、

塩水を沸騰させて
水だけを蒸発させ、
体積が２分の１になると、

塩分の濃度が２倍になる
ことと似た理屈です。

以上のことから、

１分間に作られる原尿量(ｍＬ)は、
１分間に作られる尿量(１ ｍＬ)の
１２０倍であり、

１ mL ×１２０ ＝ １２０ mL

であると計算できます。

さて、
この最後の式を
抽象化すると、

原尿量
＝　尿量　×　尿中のイヌリン濃度 / ”原尿中”のイヌリン濃度

となります。

ここで、
ろ過される物質である
イヌリンでは、

血しょう中のイヌリン濃度　＝　原尿中のイヌリン濃度

が成り立つのでした。

すると、
先ほどの式は、

原尿量
＝　尿量　×　尿中のイヌリン濃度 / ”血しょう中”のイヌリン濃度
＝　尿量　×　イヌリンの濃縮率

となります。

これは、先に解説した
原尿量を求める公式
そのものですね。

では最後に、確認問題に
挑戦してみましょう。

※：スマホ、タブレット端末でのご利用の方へ
記事最下部には、

「おすすめ記事」
(【最重要】2021共通テスト『生物基礎』攻略法など)

の一覧も記載してあります。

目次へ戻れるボタン

６：確認問題

確認問題１

ある人の、血しょう、原尿、尿の
イヌリン濃度を測定したところ、
下表のようであった(単位：mg/mL)。

また、腎臓で１分間に
作られる尿量は、１ mLであった。

①表中のＡに当てはまる
イヌリン濃度を答えなさい。

②１分間に作られる原尿量は
何 ｍＬ であるか求めなさい。

③１日に作られる原尿量は
何 Ｌ であるか求めなさい。
(小数点以下は、四捨五入)

解答

①０.１　②１２０ ｍＬ　③１７３ Ｌ

解説

ある人の、血しょうと原尿の
イヌリン濃度を測定したところ、
下表のようであった(単位：mg/mL)。

また、腎臓で１分間に
作られる尿量は、１ mLであった。

①表中のＡに当てはまる
イヌリン濃度を答えなさい。

イヌリンは、ろ過される物質なので、
　血しょう中の濃度　＝　原尿中の濃度
　となる。

　よって、０.１(mg/mL)。

②１分間に作られる原尿量は
何 ｍＬ であるか求めなさい。

１分間あたりの原尿量　
　＝　１分間あたりの尿量　×　イヌリンの濃縮率
　＝　１ ｍＬ　×　１２.０ / ０.１
　＝　１２０ ｍＬ
　と求まる。

③１日に作られる原尿量は
何 Ｌ であるか求めなさい。
(小数点以下は、四捨五入)

１分間に作られる
　原尿量が１２０ ｍＬ。

　１日は、２４時間×６０分。

　よって、
　１日に作られる原尿量は、

　１２０ ｍＬ　×　２４　×　６０　÷　１０００
　≒　１７３ Ｌ

　※１０００で割っているのは、
　　単位を ｍＬ から Ｌ に直すため。

・・・・・・・・・・・・・・・・・

確認問題２

以下の文章の空欄に適する
数式や数値を答えなさい。

ある人の、血しょう、尿の
イヌリン濃度を測定すると
下表のようであった。

(単位：％)

また、１分間で作られる尿量は、
１.５ mLであった。

上の情報から、
１分間あたりの原尿量(mL)を
求めてみよう。

イヌリンは(①：ろ過、再吸収)される
物質なので、

原尿中のイヌリン濃度は、
(　②　) ％とわかる。

このことから、
イヌリンの尿中の濃度は、
原尿中の濃度の(　③　)倍になったとわかる。

イヌリンは、
(④：ほとんど、全く)再吸収されない
物質であることから、

原尿中のイヌリンの質量と
尿中のイヌリンの質量は

等しくなる。

よって、
イヌリン濃度が(　③　)倍に
変化したことは、

尿の水量(尿量)が
原尿の水量(原尿量)の
(⑤：１２０倍、１/１２０)に
変化したことによると考えてよい。

１分間に作られる
尿量は１.５ ｍＬなので、

１分間で作られる原尿量は、
(　⑥　)ｍＬと求まる。

解答

(単位：％)

１分間で作られる尿量は、
１.５ mLであった。

上の情報から、
１分間あたりの原尿量(mL)を
求めてみよう。

イヌリンは(①：ろ過)される
物質なので、

原尿中のイヌリン濃度は、
(②：０.０１) ％とわかる。

このことから、
イヌリンの尿中の濃度は、
原尿中の濃度の(③：１２０)倍になったとわかる。

イヌリンは、
(④：全く)再吸収されない
物質であることから、

原尿中のイヌリンの質量と
尿中のイヌリンの質量は

等しくなる。

よって、
イヌリン濃度が(③：１２０)倍に
変化したことは、

尿の水量(尿量)が
原尿の水量(原尿量)の
(⑤：１/１２０)に
変化したことによると考えてよい。

１分間に作られる
尿量は１.５ ｍＬなので、

１分間で作られる原尿量は、
(⑥：１８０)ｍＬと求まる。
※⑥：１.５×１２０

『計算問題対策の関連記事』
・腎臓⑤：再吸収量の計算、再吸収率の計算
・腎臓⑥：グルコース排出量のグラフ